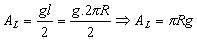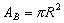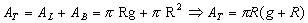Superfície esférica:
A superfície esférica de centro O e raio R é o conjunto de pontos do es[aço cuja distância ao ponto O é igual ao raio R.
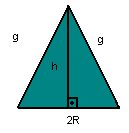
Se considerarmos a rotação completa de uma semicircunferência em torno de seu diâmetro, a superfície esférica é o resultado dessa rotação.
A área da superfície esférica é dada por:
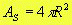
Zona esférica:
É a parte da esfera gerada do seguinte modo:
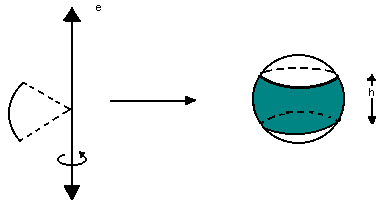
A área da zona esférica é dada por:
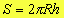
Calota esférica:
É a parte da esfera gerada do seguinte modo:
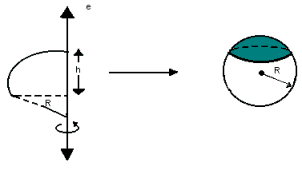
Ä área da calota esférica é dada por:
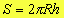
Fuso esférico:
O fuso esférico é uma parte da superfície esférica que se obtém ao girar uma semi-circunferência de um ângulo
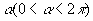
em torno de seu eixo:
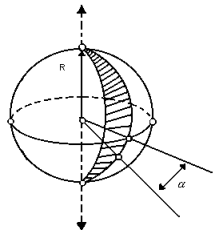
A área do fuso esférico pode ser obtida por uma regra de três simples:
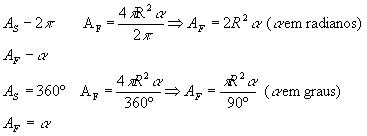
Cunha esférica:
Parte da esfera que se obtém ao girar um semicírculo em torno de seu eixo de um ângulo
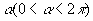
:
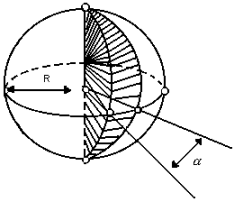
O volume da cunha pode ser obtido por uma regra de três simples:
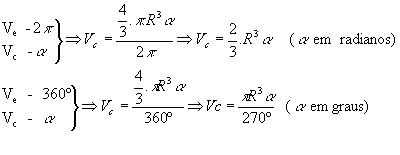
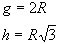
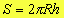

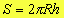
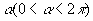 em torno de seu eixo:
em torno de seu eixo:
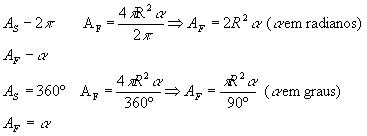
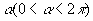 :
:
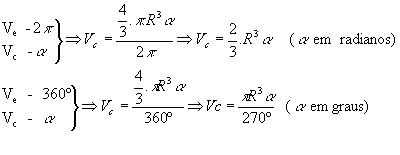
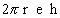 :
: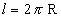 :
: