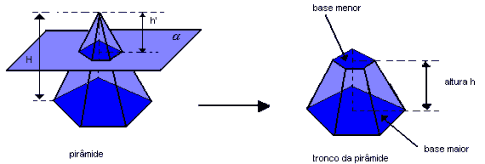
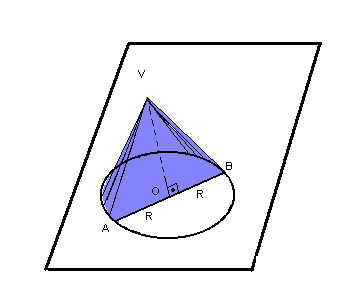
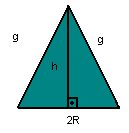
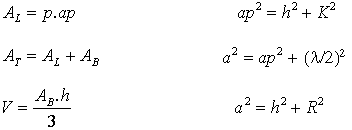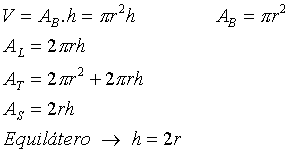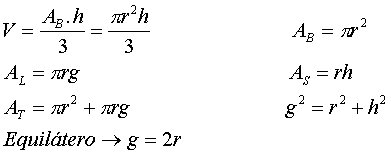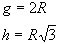Se um plano interceptar todas as arestas de uma pirâmide ou de um cone, paralelamente às suas bases, o plano dividirá cada um desses sólidos em dois outros.
Sendo o tronco do cone circular regular a seguir, temos:
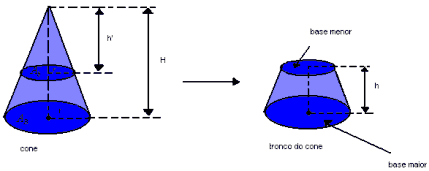
- as bases maior e menor são paralelas;
- a altura do tronco é dada pela distância entre os planos que contém as bases.